Информация и ее кодирование

 

Пример (№ 1)

  Каждый символ в Unicode закодирован двухбайтным словом. Оцените информационный объем следующего предложения в этой кодировке:

Без труда не вытащишь рыбку из пруда.

1) 37 бит           2) 592 бита      3) 37 байт        4) 592 байта

   Решение:   Длина фразы составляет примерно 40 символов. Следователь­но, ее объем можно приблизительно оценить в 40 х 2 -80 байт. Такого варианта ответа нет, попробуем перевести результат в би­ты: 80 байт х 8 - 640 бит. Наиболее близкое значение из пред­ложенных — 592 бита. Заметим, что разница между 640 и 592 составляет всего 48/16 = 3 символа в заданной кодировке и его можно считать несущественным по сравнению с длиной строки.

Ответ: 2.

  Замечание: Подсчетом символов в строке можно убедиться, что их ровно 37 (включая точку и пробелы), поэтому оценка 592 бита = 74 байта, что соответствует ровно 37 символам в двухбай­товой кодировке, является точной.

    При выполнении заданий, подобных № 4—10, следует пользо­ваться формулой алфавитного подхода к измерению количества информации I = M log₂N, где N — количество символов (мощ­ность) алфавита, в котором записано сообщение, М — количество символов в записи сообщения (длина сообщения), I — количество бит информации, содержащееся в сообщении. Если log₂N не яв­ляется целым числом, то I округляется в большую сторону.

  Информационный объем сообщения, выраженный в битах и минимальное количество двоичных разрядов, требуемое для записи сообщения в двоичном алфавите совпадают.

   Из приведенной формулы легко получить следующее след­ствие: с помощью п двоичных разрядов (бит) можно закодировать двоичным кодом все элементы множества мощностью 2n (т.е. со стоящего из 2n элементов). Информационный объем одного сим­вола алфавита, обозначающего элемент данного множества, будет равен п.

Пример (№ 2)

   Метеорологическая станция ведет наблюдение за влажностью воздуха. Результатом одного измерения является целое число от О до 100%, которое записывается при помощи минимально воз­можного количества бит. Станция сделала 80 измерений. Опреде­лите информационный объем результатов наблюдений.

1) 80 бит            2) 70 байт        3) 80 байт        4) 560 байт

Решение:

Способ 1

  Алфавитом в данном случае является множество целочисленных значений влажности от 0 до 100. Таких значений 101. Поэтому, информа­ционный объем результатов одного измерения I=log₂101. Это зна­чение не будет целочисленным. Не вычисляя его, сразу найдем округленное в большую сторону целое значение. Заметим, что ближайшая к 101 целая степень двойки, большая 101, есть чис­ло 128=2⁷. Поэтому принимаем I=log,128 = 7 бит. Учитывая, что станция сделала 80 измерений, общий информационный объем равен 80 х 7=560 бит =70 байт.

Ответ: 2.

Способ 2 

   Воспользуемся следствием из формулы. Заметим, (что 2⁶< 101 < 2⁷, поэтому минимально необходимое количество двоичных разрядов (бит) равно 7. Далее аналогично получаем, что общий информационный объем равен 80 х 7 = 560 бит=70 байт.

Ответ: 2.

Пример (№ 3)

  При выполнении заданий, связанных с понятием скорости передачи данных (№ 29—32), часто допускаются ошибки, связан­ные с неверным использованием размерности единиц измерения. Следует следить за размерностью исходных данных и размерно­стью, в которой требуется записать результат. Для успешного вы­полнения заданий такого типа нужно потренироваться в переводе Кбит/мин в Кбайт/с и т.д.

  Скорость передачи данных через ADSL-соединение равна 256 000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.

  Решение:  Размер файла = скорость х время передачи. Выразим время в секундах, а скорость — в килобайтах в секунду.

  Размер файла = 256 000/(8 1024)* 3*60 Кбайт.

  Прежде чем выполнять действия, выделим в явном виде, там, где это очень просто, степени двойки.

  Размер файла = 2⁸ / 1000/(2³ * 2¹⁰) * 3 * 15 * 4 = 2⁸ * 125 * 2³/ (2³ - 2^|(|) * 45* 2² = 2¹³ * 125 * 45/2¹³ = 125 * 45 = 5625 Кбайт.

Ответ: 5625.

  Важное замечание: Практически во всех заданиях можно избежать громоздких вычислений, упростив выражения, как это показано выше. Такая техника вычислений обязательно должна быть отработана в процессе подготовки к экзамену, поскольку она обеспечивает существенную экономию времени и минимум досадных арифметических ошибок.

 

Алгоритмизация и программирование

Пример (№ 4)

  Цепочки символов (строки) создаются по следующему правилу. Первая строка состоит из одного символа — цифры «1». Каждая из последующих цепочек создается такими действия­ми: в очередную строку дважды записывается цепочка цифр изпредыдущей строки (одна за другой, подряд), а в конец приписы­вается еще одно число — номер строки по порядку (на i-м шаге дописывается число «i»).

Вот первые 4 строки, созданные по этому правилу:

1)1

2)      112

3)      1121123

4)      112112311211234

Какая цифра стоит в седьмой строке на 121-м месте (считая слева направо)?

  Решение:  Найдем длину седьмой строки. По условию, длина каждой последующей строки увеличивается в 2 раза, по сравнению с предыдущей, плюс еще один символ — цифра, обозначающая порядковый номер самой строки.

Получается, что длина строк составит:

1) 1 элемент в строке;

2)      1x2 + 1 = 3 элемента в строке;

3)3x2 + 1 = 7;

4)7x2 + 1=15;

5)15x2 + 1 = 31;

6)31x2 + 1 = 63;

7) 63x2 + 1 = 127 элементов в строке.

  Требуется найти 121-й элемент в строке длиной в 127 симво­лов. Это означает, что нам нужен седьмой элемент с конца. По­скольку в конец строки на каждом шаге добавляется его номер (совпадающий с номером формируемой строки), то последние семь символов 7-й строки будут 1234567. Таким образом, седьмой символ с конца — единица.

Ответ: 1.

  Для быстрого и успешного выполнения рассмотренного зада­ния важно было не механически выполнить алгоритм, а понять закономерность, которую он выражает, и, воспользовавшись ей, найти решение.

  Важное замечание: Практически во всех заданиях на исполнение алгоритмов можно избежать большого объема рутинной работы, выявив закономерность, реализуемую алгоритмом.

Пример (№ 5)

  Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существуют две команды: (Вперед п, вызывающая передвижение Черепашки на п шагов в направлении движения. Направо т, вызывающая изменение направления движения на т градусов по часовой стрелке. О < т < 180, вместо n и т должны стоять целые числа).

Запись:

  Повтори 5 [Команда1 Команда2] означает, что последова­тельность команд в квадратных скобках повторится 5 раз. Какое число необходимо записать вместо п в следующем алгоритме: Повтори 6 [Вперед 40 Направо n], чтобы на экране появился правильный пятиугольник.

  Решение: Сумма внутренних углов правильного пятиугольника вы­числяется по формуле (р-2) х180, где р -5. Поэтому величина одного внутреннего угла будет равна (5 - 2) х 180/5 = 108°. А угол поворота Черепашки в вершине пятиугольника будет равен углу, смежному с внутренним углом, т.е. 180-108 = 72°.

  Черепашка прочертит на экране 6 отрезков, но последний от­резок полностью совпадет с первым, так как после пятого выпол­нения цикла Черепашка полностью обернется вокруг своей оси (72 x 5 = 360°) и окажется в той же точке, что и изначально. Так что на экране появится правильный пятиугольник.

Ответ: 72.

 

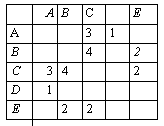
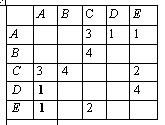
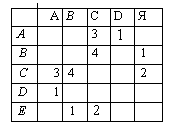
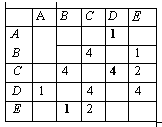
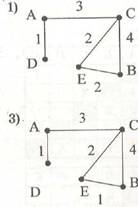
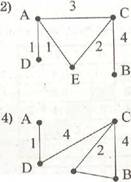
Моделирование

Пример (№ 6)

   Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, озна­чают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.

  Укажите таблицу, для которой выполняется условие: «Мини­мальная стоимость проезда из А в Б не больше 6».

  Стоимость проезда по маршруту складывается из стои­мостей проезда между соответствующими соседними станциями.

1)	2)
3)	4)

  Решение:  Построим схемы, соответствующие каждой таблице:

  Видно, что минимальная стоимость проезда из А в В дости­гается на схеме 3 на маршруте АСЕВ, и она равна 6, т.е. условие задания выполнено.

Ответ: 3.